Miscellaneous Information
Derivation of Observation Parameters and Sensitivity
Suppose a mapping area of
l1 ["] ![]() l2 ["]
(l1 along the scan, l2 across the scan).
Time to be taken in a scan row (on-source) is
tscan [s];
scan speed on the celestial sphere is
vscan ["/s] =
l1/tscan;
separation between the scan rows is
l2 ["]
(l1 along the scan, l2 across the scan).
Time to be taken in a scan row (on-source) is
tscan [s];
scan speed on the celestial sphere is
vscan ["/s] =
l1/tscan;
separation between the scan rows is
![]() l ["];
number of scan rows is
Nrow =
l2/
l ["];
number of scan rows is
Nrow =
l2/![]() l (+1); and
the grid spacing of a map to be made is
d ["]
l (+1); and
the grid spacing of a map to be made is
d ["] ![]() d ["].
And we call the number of on-source scans per one OFF as NscanSEQ.
d ["].
And we call the number of on-source scans per one OFF as NscanSEQ.
In this situation, total on-source scan time becomes
![]() .
.
The total time spent to run a observe table
including OFF, R-SKY, antenna slew, etc. is estimated to be
![]() ,
,
where
tOFF [s] is an integration time for one OFF, and
fcal is an overhead of R-SKY calibration
(if you use 1 minute to obtain R-SKY at every 15 minutes, fcal=16/15).
tOH [s] is an overhead time per one scan row, which consists of
go and return to the OFF point
2![]() ttranOFF
(the time for one-way move to OFF point ttranOFF is typically 5[s]),
time for approach run
tapp [s] (4[s] is recommended), and
time for transit run
ttran [s] (2[s] is recommended),
thus is written as
ttranOFF
(the time for one-way move to OFF point ttranOFF is typically 5[s]),
time for approach run
tapp [s] (4[s] is recommended), and
time for transit run
ttran [s] (2[s] is recommended),
thus is written as
![t_{\rm OH} = \frac{2t_{\rm tran}^{\rm OFF}}{N_{\rm scan}^{\rm SEQ}} + t_{\rm app} + \frac{N_{\rm scan}^{\rm SEQ}-1}{N_{\rm scan}^{\rm SEQ}} t_{\rm tran} = 6+\frac{8}{N_{\rm scan}^{\rm SEQ}}\;[{\rm s}]\mbox{ (for ASTE)}](images/toh.gif)
Now the ratio of on-source time to the total time spent is
![]() .
.
The total ON-source integration time for a map grid point is a sum of time during which the beam(s) scans within the grid.
Effectively a factor ![]() is multiplied and it becomes
is multiplied and it becomes
![]() .
.
The factor ![]() is a constant
determined by the type and parameters of the convolution function and is calculated as follows.
Suppose that observed points i = 1,2,... are uniformly distributed around the grid point and
each point has a spectrum of Ti(k)
[k = 1,..,Nch],
rms noise temperature of
is a constant
determined by the type and parameters of the convolution function and is calculated as follows.
Suppose that observed points i = 1,2,... are uniformly distributed around the grid point and
each point has a spectrum of Ti(k)
[k = 1,..,Nch],
rms noise temperature of ![]() i , and
a weight of the convolution function of wi .
We assume the on-source integration time t0 and
the noise temperature
i , and
a weight of the convolution function of wi .
We assume the on-source integration time t0 and
the noise temperature ![]() i =
i = ![]() 0 =
Tsys/sqrt(B t0)
of each point to be constant.
The convolved spectrum T(k) is written as
T =
(
0 =
Tsys/sqrt(B t0)
of each point to be constant.
The convolved spectrum T(k) is written as
T =
(![]() wiTi)/(
wiTi)/(![]() wi) ,
and its noise temperature
wi) ,
and its noise temperature ![]() becomes
becomes
![]() = sqrt(
= sqrt(![]() wi2)/
wi2)/![]() wi
wi ![]()
![]() 0
= Tsys/sqrt(B tcellON)
[here tcellON
0
= Tsys/sqrt(B tcellON)
[here tcellON ![]() (
(![]() wi)2/
wi)2/![]() (wi2)
(wi2)
![]() t0 ].
If we take the grid spacing as the unit of spacial length and redefine
t0 as the on-source integration time per unit area (1 grid cell),
summations can be rewritten with integrals: tcellON =
(
t0 ].
If we take the grid spacing as the unit of spacial length and redefine
t0 as the on-source integration time per unit area (1 grid cell),
summations can be rewritten with integrals: tcellON =
(![]() w dx dy)2/
w dx dy)2/![]() w2dx dy
w2dx dy
![]() t0
t0 ![]()
![]() t0 .
The values of
t0 .
The values of ![]() for convolution functions Bessel*Gauss, Sinc*Gauss, Gauss, Pillbox, and Spheroidal
with default parameters are, respectively, 4.3, 1.2, 6.3, 1.0, and 10.2.
for convolution functions Bessel*Gauss, Sinc*Gauss, Gauss, Pillbox, and Spheroidal
with default parameters are, respectively, 4.3, 1.2, 6.3, 1.0, and 10.2.
Assuming that the system noise temperature is Tsys [K] and
the spectral resolution of a map to be made is B [Hz],
the noise (of the map) due to on-source integrations is estimated to be
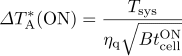 ,
,
where ![]() q is the quantization efficiency of the spectrometer.
For the MAC (ACG)
q is the quantization efficiency of the spectrometer.
For the MAC (ACG)
![]() q=0.88,
while it is 0.64 for the WHSF.
On the other hand, the number of OFF points used to consist a map grid point is about
1+(d-
q=0.88,
while it is 0.64 for the WHSF.
On the other hand, the number of OFF points used to consist a map grid point is about
1+(d-![]() l)/
(NscanSEQ
l)/
(NscanSEQ![]() l)
[in fact the effective number of OFF points is larger than this value, since the convolution function spreads out of the cell.
Taking this into account, the optimum OFF-point integration time becomes smaller by a factor of, roughly,
l)
[in fact the effective number of OFF points is larger than this value, since the convolution function spreads out of the cell.
Taking this into account, the optimum OFF-point integration time becomes smaller by a factor of, roughly,
![]() -1/4.
The observing efficiency hardly changes].
The effective OFF integration time for a grid is
-1/4.
The observing efficiency hardly changes].
The effective OFF integration time for a grid is
![]() ,
,
and the noise due to OFF points becomes
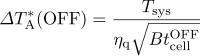 .
.
Therefore the total noise level of the map is written as
 .
.
The noise level of a map achieved in unit observation time
![]() TA*(0) is written as
TA*(0) is written as
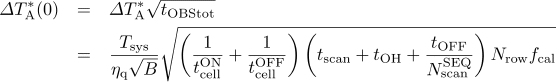 .
.
This value is minimized when tOFF is optimal:
![]()
leads to
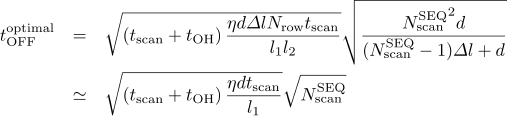 .
.
Convolution in "Make Map"
As shown in Fig. 1-2 in "Introduction", the default convolution function, Bessel*Gauss, has an FWHM of twice of the map grid spacing d. Fig. 5-1 shows responses to a point source (i.e., effective beam) when grid spacing is set to be 0.1, 0.2, ..., 1.0 times the telescope beam FWHM. Peak intensity of a point source and effective beam width varies as Fig. 5-2. For example, when the grid spacing d is a half of the beam FWHM, peak temperature of a point source decreases by a factor of 0.7, and the effective beam width becomes 1.3 times broader.
If d is too small, effective integration time for a grid (tcellON) becomes small, which leads to a large noise level. Since the spatial resolution is limited by the telescope beam, the map is too much oversampled. On the other hand, if d is too large, the effective beam width broadens to 2d as shown here. An appropriate grid spacing should be chosen according to the scientific aim.
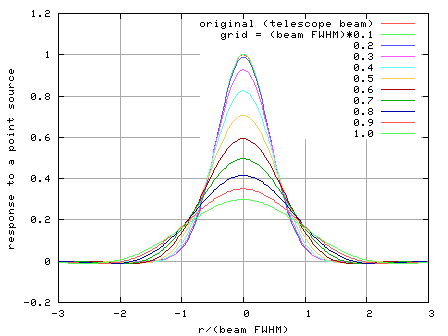
Fig. 5-1: responses to a point source (effective beam)
when grid spacing is set to be 0.1, 0.2, ..., 1.0 times the telescope beam (FWHM).
The horizontal axis is the distance from the source (normalized by the beam FWHM),
while the vertical axis is the observed intensity (normalized by the value without convolution).
The telescope beam is assumed to be a Gaussian.
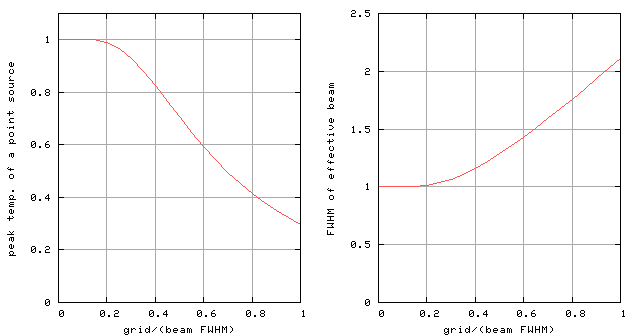
Fig. 5-2: Variations of
(left) peak intensity of a point source,
(right) effective beam width (FWHM)
when the grid spacing (the horizontal axis) varies from 0 to 1 times the beam FWHM.
The vertical axes is normalized by the value without convolution.
A C program which calculates an effective beam. The telescope beam size, grid spacing, and type of convolution function can be specified.
GLS Projection in "Make Map" and WCS
When a map is made, celestial (spherical) coordinate values are projected onto an X-Y (planar) coordinate pixel values. By default, global sinusoidal projection (GLS) is applied: i.e., celestial coordinate (RA,DEC) is transferred into (X,Y) as
sin(X/2) = sin((RA-RA0)/2)*cos(DEC)
Y = DEC-DEC0
where (RA0,DEC0) is a reference position [in general, source position defined in the "Source Table"]. The Galactic coordinate (l,b) is also converted to (X,Y) in the same way.
Coordinate headers of FITS cubes written by the "Make Map" task follow the AIPS format:
CRVAL1 = RA0
CRPIX1 = 1 - XBLC/CDELT1 = 1 - (2*asin(sin((RABLC-RA0)/2)*cos(DEC)))/CDELT1
CRVAL2 = DEC0
CRPIX2 = 1 - YBLC/CDELT2 = 1 - (DECBLC-DEC0)/CDELT2
Here it should be noted that the center of projection is not (RA0,DEC0), but (RA0,0). It differs from the World Coordinate System (WCS) manners, thus you have to take care if you would like to convert the coordinate values into WCS [it is also noted in footnote 2 of the AIPS Memo 46 "Additional Non-linear Coordinates in AIPS"].
Bit Number of Spectrum Data
OTF raw data has a dynamic range of 12 bits (4096 levels). Though the bit number is smaller than that of NewStar raw data (32 bit; 4.3 billion levels), it is unavoidable to reduce bit number because data production rate is quite high. Since the signal-to-noise ratio of individual spectrum taken with OTF is low due to very short (0.1 s) integration, sensitivity loss due to the quantumization is, in general, negligible. However, the data may be affected in the following situation: an extremely (really extremely) strong spurious signal appears or bandpass becomes nearly 0 (i.e., TA* diverges) in the bandwidth.
Doppler Correction
In OTF observations with ASTE, Doppler correction for vrad (relative motion of the telescope with respect to the LSR/Heliocentric system) is done in the data production ("merge") process after the observations. That is, LO frequency shift according to the change of vrad is not performed during the observations. At first (ON-OFF)/(R-SKY) operation is performed channel by channel from the raw output from the spectrometer (R, SKY, OFF, and ON), and then resampling along the frequency axis according to vrad for each ON point is done. If there is emission at OFF point, the it appears like an absorption profile in the resultant spectrum. The velocity of "absorption" feature gradually shift according to vrad of ON point. This effect is hard to be corrected: it should be checked carefully enough that there is no emission at the OFF point.
If we calculate (ON-OFF)/(R-SKY) after resampling R, SKY, OFF, and ON along the frequency individually, OFF-point emission will appear as an absorption in a constant velocity. However, this procedure cannot be adopted since the "differential" of the band characteristics heavily affects the spectral baseline.
FAQ
- Q: Blank value is written in my FITS cube. Why?
- A: Blank is written when there are not sufficient number ("Minimum number of data" in the Map GUI) around the grid point. Caution: the map command skips spectra whose baselines are not subtracted yet.
- Q: I have mistook the IF configuration and the frequency shifted. What should I do?
- A: The data may become usable by (1) rewriting header FRQ00 to the frequency which has been actually observed, and (2) specifying a reference frequency (rest frequency of the line) when executing the Map command. The header can be modified using the task "Modify Header" in the button panel.
- Q: Is there an Export version of the reduction software package?
- A: Yes, there is. See "Export version of NOSTAR" in the site of NRO 45-m telescope.
- Q: OK, then, does OTF really improve the efficiency?
- A: Suppose that we obtain the same map (the same grid, the same resolution) as
How to Determine Parameters: An Example with the position-switch.
To cover the area of 300"
 300"
with a spacing of 7.5", 1681 points are observed.
If we employ 1** (OFF-ON-ON) sequence, it will take about 20 hours to observe the entire region.
Making convolution to match the spatial resolution to OTF, effective integration time becomes 4.3 times longer,
tON=tOFF=86 [sec], thus
300"
with a spacing of 7.5", 1681 points are observed.
If we employ 1** (OFF-ON-ON) sequence, it will take about 20 hours to observe the entire region.
Making convolution to match the spatial resolution to OTF, effective integration time becomes 4.3 times longer,
tON=tOFF=86 [sec], thus
 TA*
=
TA*
= 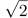 Tsys /
Tsys /
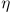 qsqrt(B tON)
= 0.087 [K].
Here we compare the noise level achieved in an unit observation time (1 hour)
qsqrt(B tON)
= 0.087 [K].
Here we compare the noise level achieved in an unit observation time (1 hour)
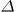 TA*(0):
for OTF it is 0.35
TA*(0):
for OTF it is 0.35 sqrt(41/60)=0.29 [K], and
for position switch it becomes 0.087
sqrt(41/60)=0.29 [K], and
for position switch it becomes 0.087 sqrt(20)=0.39 [K].
Therefore, OTF is more efficient by a factor of (0.39/0.29)2=1.8.
We have already confirmed that, for OTF observations, the noise level calculated here is very close to that of actual data.
In short --- definitely YES, unless you are planning extremely inefficient OTF observations.
sqrt(20)=0.39 [K].
Therefore, OTF is more efficient by a factor of (0.39/0.29)2=1.8.
We have already confirmed that, for OTF observations, the noise level calculated here is very close to that of actual data.
In short --- definitely YES, unless you are planning extremely inefficient OTF observations.