How to Determine Parameters

Determining Parameters and Sensitivities

You can determine observation parameters and estimate sensitivities in the following way. See Fig. 1-1 in "Introduction" to understand meanings of variables to appear below.

#Derivation of equations is shown in "Miscellaneous Information".

At first you should set fundamental parameters listed below:

The dimension of the mapping area l₁ ["] 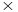$\times$ l₂ ["] (l₁ along the scan, l₂ across the scan).
Time to be taken in a scan row (on-source) t_scan [s] : scan speed on the celestial sphere then becomes v_scan ["/s] = l₁/t_scan .
- t_scan should be chosen so that the antenna does not move more than 1/3 or 1/4 of HPBW during the data dump (integration) time t_dump [s], 0.1 (ACG) or 0.2 (WHSF) sec.
- See Hints on Choosing Parameters.
Set the number of on-source scans per one OFF N_scan^SEQ; separation between the scan rows 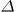l ["]; and the grid spacing of a map to be made d ["] 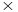d ["]. Now the number of scan rows is written as N_row = l₂/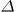 l +1 .
- We recommend to set 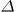${\mit\Delta}$ l to be about 1/3 of HPBW, and d to be 1/3 -- 1/2 of HPBW.
- See Hints on Choosing Parameters.

Using these values, parameters and the sensitivity are determined as follows. You can calculate them using a tool (otfaste.pl).

An overhead time per one scan row t_OH [s] is written as t_OH = 6 + 8/N_scan^SEQ .
Determine an optimal OFF-point integration time t_OFF [s] as
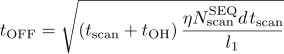$t_{\rm OFF} = \sqrt{\left(t_{\rm scan}+t_{\rm OH} \right) \frac{\eta N_{\rm scan}^{\rm SEQ} d t_{\rm scan}}{l_1}}$ .
Here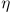 $\eta$ =4.3 (It depends on the type and parameters of convolution function. With the default parameters, it becomes 4.3 for Bessel*Gauss, 1.2 for Sinc*Gauss, 6.3 for Gauss, 1.0 for Pillbox, 10.2 for Spheroidal. See Miscellaneous Information: Derivation of Observation Parameters and Sensitivity).
The total time spent to run a observe table including OFF, R-SKY, antenna slew, etc. is estimated to be
.
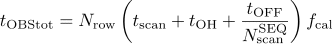Here f_cal is an overhead to obtain R-SKY calibration data (if you use 1 minute at every 15 minutes, f_cal=16/15).
- If t_OBStot becomes larger than the interval between pointing observations, you have to reduce t_OBStot by, e.g., divide the mapping area into multiple observation tables.
The total on-source time is
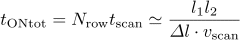$t_{\rm ONtot} = N_{\rm row}t_{\rm scan} \simeq \frac{l_1 l_2}{{\mit\Delta}l \cdot v_{\rm scan}}$ .
The effective integration times of ON and OFF for a map grid are written as, respectively,
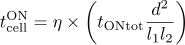
$t_{\rm cell}^{\rm ON} = \eta \times \left( t_{\rm ONtot} \frac{d^2}{l_1 l_2} \right)$
and
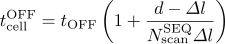$t_{\rm cell}^{\rm OFF} = t_{\rm OFF} \left( 1+\frac{d-{\mit\Delta}l}{N_{\rm scan}^{\rm SEQ}{\mit\Delta}l} \right)$ .
Using the system noise temperature T_sys [K] and the frequency resolution of the map to be made B [Hz], the rms noise temperature of the map is estimated as
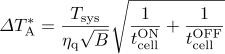${\mit\Delta}T_{\rm A}^* = \frac{T_{\rm sys}}{\eta_{\rm q}\sqrt{B}}\sqrt{\frac{1}{t_{\rm cell}^{\rm ON}}+\frac{1}{t_{\rm cell}^{\rm OFF}}}$ .
Here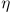 $\eta$ _q is the quantization efficiency of the spectrometer: it is 0.88 for the MAC (ACG), 0.60 for the WHSF.

Compared with the common position-switch ("step-and-integrate") observations, higher observing efficiency is expected to be acheived in OTF observations due to the following facts:

The ratio of on-source time to the total time spent 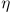$\eta$ _ON/OBS = t_ONtot/t_OBStot becomes larger because not only the dead time is reduced, but also optimum OFF point integration time is relatively shorter (t_OFF < t_scan).
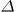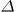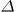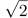
In general t_cell^ON < t_cell^OFF, thus ${\mit\Delta}$ T_A^* nearly equals to ${\mit\Delta}$ T_A^*(ON) (for position-switch observations, ${\mit\Delta}$ T_A^* $\simeq$ $\sqrt{2}$ ${\mit\Delta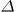}$ T_A^*(ON) ).

See Miscellaneous Information: FAQ section: an example of comparison between OTF and position-switch is shown. In case of the limit of dead time -> 0, the efficiency in time can get 4 times higher than the position-switch observations.

Hints on Choosing Parameters

As t_scan becomes long (v_scan becomes small), nominal observing efficiency increases. The upper limit of t_scan is defined by the following conditions:
- As time between OFF integrations becomes longer, baseline gets poor.
- When the time spent to cover the entire map becomes too long, the quality of the obtained map is no longer "uniform" (the uniformity is one of main advantages of OTF observations).
We have not evaluated the upper limit of duration between OFFs. But it is expected that it can be extended as those for common position-switch observations.
On the other hand, the lower limit of t_scan is defined by a condition that the sampling along the scan should be frequent enough. At least Nyquist sampling is required. We recommend to sample more frequently than 1/3--1/4 of the telescope beam in order to avoid beam smearing: i.e., t_dumpv_scan < (1/3--1/4) HPBW.
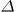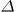Spacings between scan rows ${\mit\Delta}$ l should be smaller than the Nyquist sampling rate. Taking the antenna jitters etc. into account, oversampling is recommended (about 1/3 of the HPBW). It is also recommended to set ${\mit\Delta}$ l to be equal to or smaller than the grid spacing d.
The resultant map has so-called scanning effects if scans along only one direction are coadded. The scanning effect will be significantly reduced by combining orthogonal scans. The so-called PLAIT algorithm described by Emerson & Gräve (1988) is implemented in the data reduction software. See Data Reduction section. [The PRESS method by Sofue & Reich (1979), which is applicable to single-direction-scanned maps, is also impremented for those who could not obtain orghogonal scans.]

An Example of Parameters

Assuming to use the MAC (ACG) with parameters l₁=l₂=300 ["], t_scan=30 [s], ${\mit\Delta}$ l=7.5 ["], d=7.5 ["], T_sys(SSB)=500 [K], and B=1 [MHz]

% perl otfaste.pl.txt
### OTF sensitivity estimation for ASTE ###
backend type                            (1:MAC, 2:WHSF): 1
length of mapping area (along the scans)    l1 [arcsec]: 300
length of mapping area (perp. to the scans) l2 [arcsec]: 300
time for scan                                 tscan [s]: 30
number of ONs per OFF                        Nscan(SEQ): 1
separation between scans              (delta)l [arcsec]: 7.5
map grid                                     d [arcsec]: 7.5
system noise temperature                       Tsys [K]: 500
resolution bandwidth                            B [kHz]: 1000
--- Summary of parameters of your observation ---
Backend type                                           : MAC
Length of mapping area (along the scans)    l1 [arcsec]: 300.00
Length of mapping area (perp. to the scans) l2 [arcsec]: 300.00
Time for scan                                 tscan [s]: 30.00
Number of ONs per OFF                        Nscan(SEQ): 1
Separation between scans              (delta)l [arcsec]: 7.50
Map grid                                     d [arcsec]: 7.50
System noise temperature                       Tsys [K]: 500.00
Resolution bandwidth                            B [kHz]: 1000.000
Scan speed (1.0" per 0.1s sample)               ["/sec]: 10.0
Effective integrtion time of ON                   [sec]: 3.31
Effective integrtion time of OFF                  [sec]: 12.00
Overhead time per one scan                        [sec]: 14.0
Total on-souce time                               [min]: 20.5
Total time per one map                            [min]: 40.8
Observing efficiency eta(ON/OBS)                       : 0.50
Optimal OFF-point integration time                [sec]: 12.0 -> 12
Rms noise temperature of one map                    [K]: 0.353

The optimal OFF-integration is 12 seconds. This table will take about 40 minutes to run and ${\mit\Delta}$ T_A^*=0.35 [K] is obtained. Effective spatial resolution becomes 24" (see Miscellaneous Information: Convolution in "Make Map").

#FYI: Redirection of the standard input to a file (sample) may make recalculation much easier: e.g., perl otfaste.pl.txt < otfaste_input.txt. If you execute this script as perl otfaste.pl.txt tex, you can see an example of results of sensitivity estimation.

last update: 2015-02-20